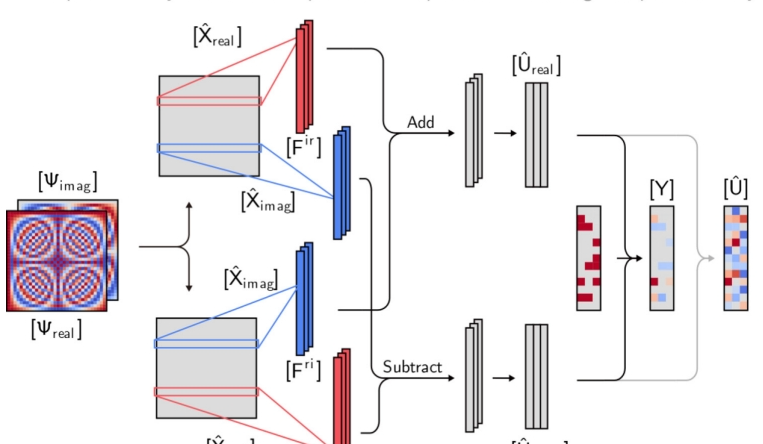
Compressive sensing has been studied and applied in structural health monitoring for data acquisition and reconstruction, wireless data transmission, structural modal identification, and spare damage identification. The key issue in compressive sensing is finding the optimal solution for sparse optimization. In the past several years, many algorithms have been proposed in the field of applied mathematics. In this article, we propose a machine learning–based approach to solve the compressive-sensing data-reconstruction problem. By treating a computation process as a data flow, the solving process of compressive sensing–based data reconstruction is formalized into a standard supervised-learning task. The prior knowledge, i.e. the basis matrix and the compressive sensing–sampled signals, is used as the input and the target of the network; the basis coefficient matrix is embedded as the parameters of a certain …
Compressive Sensing
In structural health monitoring, data quality is crucial to the performance of data-driven methods for structural damage identification, condition assessment, and safety warning. However, structural health monitoring systems often suffer from data imperfection, resulting in some entries being unusable in a data matrix. Discrete missing points are relatively easy to recover based on known adjacent points, whereas segments of continuous missing data are more common and also more challenging to recover in a practical scenario. Formulating the data recovery task as an optimization problem for matrix completion, we present a convolutional neural network to achieve simultaneous recovery for multi-channel data with the awareness of group sparsity. The data recovery process based on compressive sensing is formulated as a regression problem and achieved in the neural network. The basis matrix is utilized as the …